Chapter 10: Describing discrete-time event occurrence data • alda

library(alda)
library(dplyr)
library(tidyr)
library(purrr)
library(ggplot2)
library(patchwork)
library(survival)
library(broom)

10.1 The life table

In Section 10.1 Singer and Willett (2003) introduce the life table—the primary tool for for summarizing the sample distribution of event occurrence—using a subset of data from Singer (1993), who measured how many years 3941 newly hired special educators in Michigan stayed in teaching between 1972 and 1978. Teachers were followed for up to 13 years or until they stopped teaching in the state.

For this example we return to the teachers data set introduced in Chapter 9, a person-level data frame with 3941 rows and 3 columns:

id: Teacher ID.
years: The number of years between a teacher’s dates of hire and departure from the Michigan public schools.
censor: Censoring status.

teachers
#> # A tibble: 3,941 × 3
#>    id    years censor
#>    <fct> <dbl>  <dbl>
#>  1 1         1      0
#>  2 2         2      0
#>  3 3         1      0
#>  4 4         1      0
#>  5 5        12      1
#>  6 6         1      0
#>  7 7        12      1
#>  8 8         1      0
#>  9 9         2      0
#> 10 10        2      0
#> # ℹ 3,931 more rows

As Singer and Willett (2003) discuss, a life table tracks the event histories of a sample of individuals over a series of contiguous intervals—from the beginning of time through the end of data collection—by including information on the number of individuals who:

Entered each interval.
Experienced the target event during an interval.
Were censored at the end of an interval.

We can either construct a life table “by hand” by first converting the person-level data set to a person-period data set, then cross-tabulating time period and event-indicator variables; or by using a prepackaged routine. Because we will be constructing a life table “by hand” in Section 10.5, here we demonstrate the prepackaged routine approach.

Conceptually, the life table is simply the tabular form of a survival function (see Section 10.2); thus, an easy way to construct a life table is to first fit a survival function to the person-level data set, then use the summary of the fit as a starting point to construct the remainder of the table.

We can fit a survival function using the survfit() function from the survival package. The model formula for the survfit() function takes the form response ~ terms, where the response must be a “survival object” created by the Surv() function. For right-censored data, the survival object can be created by supplying two unnamed arguments to the Surv() function corresponding to time and event variables, in that order. Note that we can recode a censor variable into an event variable by reversing its values. For 0-1 coded data, we can write the event status as event = censor - 1.

teachers_fit <- survfit(Surv(years, 1 - censor) ~ 1, data = teachers)

summary(teachers_fit)
#> Call: survfit(formula = Surv(years, 1 - censor) ~ 1, data = teachers)
#> 
#>  time n.risk n.event survival std.err lower 95% CI upper 95% CI
#>     1   3941     456    0.884 0.00510        0.874        0.894
#>     2   3485     384    0.787 0.00652        0.774        0.800
#>     3   3101     359    0.696 0.00733        0.682        0.710
#>     4   2742     295    0.621 0.00773        0.606        0.636
#>     5   2447     218    0.566 0.00790        0.550        0.581
#>     6   2229     184    0.519 0.00796        0.504        0.535
#>     7   2045     123    0.488 0.00796        0.472        0.504
#>     8   1642      79    0.464 0.00800        0.449        0.480
#>     9   1256      53    0.445 0.00811        0.429        0.461
#>    10    948      35    0.428 0.00827        0.412        0.445
#>    11    648      16    0.418 0.00848        0.401        0.435
#>    12    391       5    0.412 0.00870        0.396        0.430

Next, we’ll collect the summary information from the survfit object into a tibble using the tidy() function from the broom package. For now we will exclude any statistical summaries from the life table, focusing exclusively on columns related to the event histories of the teachers data. Note also that the summary information from the survfit object starts at the time of the first event, not the “beginning of time”. We can add a “beginning of time” to the survfit object using the survfit0() function from the survival package, which (by default) adds a starting time of 0 to the life table.

teachers_lifetable <- teachers_fit |>
  survfit0() |>
  tidy() |>
  select(-c(estimate:conf.low)) |>
  mutate(interval = paste0("[", time, ", ", time + 1, ")"), .after = time) |>
  rename(year = time)

teachers_lifetable
#> # A tibble: 13 × 5
#>     year interval n.risk n.event n.censor
#>    <dbl> <chr>     <dbl>   <dbl>    <dbl>
#>  1     0 [0, 1)     3941       0        0
#>  2     1 [1, 2)     3941     456        0
#>  3     2 [2, 3)     3485     384        0
#>  4     3 [3, 4)     3101     359        0
#>  5     4 [4, 5)     2742     295        0
#>  6     5 [5, 6)     2447     218        0
#>  7     6 [6, 7)     2229     184        0
#>  8     7 [7, 8)     2045     123      280
#>  9     8 [8, 9)     1642      79      307
#> 10     9 [9, 10)    1256      53      255
#> 11    10 [10, 11)    948      35      265
#> 12    11 [11, 12)    648      16      241
#> 13    12 [12, 13)    391       5      386

As Singer and Willett (2003) discuss, we interpret the columns of the life table as follows:

year: Defines the time of each interval using ordinal numbers.
interval: Defines precisely which event times appear in each interval using the interval notation, [start, end), where each interval includes the starting time and excludes the ending time.
n.risk: Defines the risk set during each interval; that is, the number of (remaining) individuals who are eligible to experience the target event during an interval.
n.event: Defines the number of individuals who experienced the target event during an interval.
n.censor: Defines the number of individuals who were censored during an interval.

Importantly, notice that once an individual experiences the target event or is censored during an interval, they drop out of the risk set in all future intervals; thus, the risk set is inherently irreversible.

10.2 A framework for characterizing the distribution of discrete-time event occurrence data

In Section 10.2 Singer and Willett (2003) introduce three statistics for summarizing the event history information of the life table, which can estimated directly from the life table:

Hazard is the fundamental quantity used to assess the risk of event occurrence in each discrete time period. The discrete-time hazard function is the conditional probability that the $i$ th individual will experience the target event in the $j$ th interval, given that they did not experience it in any prior interval:

$h(t_{ij}) = \Pr[T_i = j \mid T \geq j],$

whose maximum likelihood estimates are given by the proportion of each interval’s risk set that experiences the event during that interval:

$\hat h(t_j) = \frac{n \text{ events}_j}{n \text{ at risk}_j}.$
The survival function is the cumulative probability that the $i$ th individual will not experience the target event past the $j$ th interval:

$S(t_{ij}) = \Pr[T > j],$

whose maximum likelihood estimates are given by the cumulative product of the complement of the estimated hazard probabilities across the current and all previous intervals:

$\hat S(t_j) = [1 - \hat h(t_j)] [1 - \hat h(t_{j-1})] [1 - \hat h(t_{j-2})] \dots [1 - \hat h(t_1)].$
The median lifetime is a measure of central tendency identifying the point in time by which we estimate that half of the sample has experienced the target event and half has not, given by:

$\text{Estimated median lifetime} = m + \Bigg[ \frac{\hat S(t_m) - .5}{\hat S(t_m) - \hat S(t_{m + 1})} \Bigg] \big( (m + 1) - m \big),$

where $m$ is the time interval immediately before the median lifetime, $\hat S(t_m)$ is the value of the survivor function in the $m$ th interval, and $\hat S(t_{m + 1})$ is the value of the survivor function in the next interval.

Using the life table to estimate hazard probability, survival probability, and median lifetime

First, the discrete-time hazard function and the survival function. Note the use of if-else statements to provide preset values for the “beginning of time”, which by definition will always be NA for the discrete-time hazard function and 1 for the survival function.

teachers_lifetable <- teachers_lifetable |>
  mutate(
    haz.estimate = if_else(year != 0, n.event / n.risk, NA),
    surv.estimate = if_else(year != 0, 1 - haz.estimate, 1),
    surv.estimate = cumprod(surv.estimate)
  )

# Table 10.1, page 327:
teachers_lifetable
#> # A tibble: 13 × 7
#>     year interval n.risk n.event n.censor haz.estimate surv.estimate
#>    <dbl> <chr>     <dbl>   <dbl>    <dbl>        <dbl>         <dbl>
#>  1     0 [0, 1)     3941       0        0      NA              1    
#>  2     1 [1, 2)     3941     456        0       0.116          0.884
#>  3     2 [2, 3)     3485     384        0       0.110          0.787
#>  4     3 [3, 4)     3101     359        0       0.116          0.696
#>  5     4 [4, 5)     2742     295        0       0.108          0.621
#>  6     5 [5, 6)     2447     218        0       0.0891         0.566
#>  7     6 [6, 7)     2229     184        0       0.0825         0.519
#>  8     7 [7, 8)     2045     123      280       0.0601         0.488
#>  9     8 [8, 9)     1642      79      307       0.0481         0.464
#> 10     9 [9, 10)    1256      53      255       0.0422         0.445
#> 11    10 [10, 11)    948      35      265       0.0369         0.428
#> 12    11 [11, 12)    648      16      241       0.0247         0.418
#> 13    12 [12, 13)    391       5      386       0.0128         0.412

Then the median lifetime. Here we use the slice() function from the dplyr package to select the time intervals immediately before and after the median lifetime, then do a bit of wrangling to make applying the median lifetime equation easier and clearer.

teachers_median_lifetime <- teachers_lifetable |>
  slice(max(which(surv.estimate >= .5)), min(which(surv.estimate <= .5))) |>
  mutate(m = c("before", "after")) |>
  select(m, year, surv = surv.estimate) |>
  pivot_wider(names_from = m, values_from = c(year, surv)) |>
  summarise(
    surv.estimate = .5,
    year = year_before
      + ((surv_before - .5) / (surv_before - surv_after))
      * (year_after - year_before)
  )
  
teachers_median_lifetime
#> # A tibble: 1 × 2
#>   surv.estimate  year
#>           <dbl> <dbl>
#> 1           0.5  6.61

A valuable way of examining these statistics is to plot their trajectories over time.

teachers_haz <- ggplot(teachers_lifetable, aes(x = year, y = haz.estimate)) +
  geom_line() +
  scale_x_continuous(breaks = 0:13) +
  coord_cartesian(xlim = c(0, 13), ylim = c(0, .15))

teachers_surv <- ggplot(teachers_lifetable, aes(x = year, y = surv.estimate)) +
  geom_line() +
  geom_segment(
    aes(xend = year, y = 0, yend = .5),
    data = teachers_median_lifetime,
    linetype = 2
  ) +
  geom_segment(
    aes(xend = 0, yend = .5),
    data = teachers_median_lifetime,
    linetype = 2
  ) +
  scale_x_continuous(breaks = 0:13) +
  scale_y_continuous(breaks = c(0, .5, 1)) +
  coord_cartesian(xlim = c(0, 13))

# Figure 10.1, page 333:
teachers_haz + teachers_surv + plot_layout(ncol = 1, axes = "collect")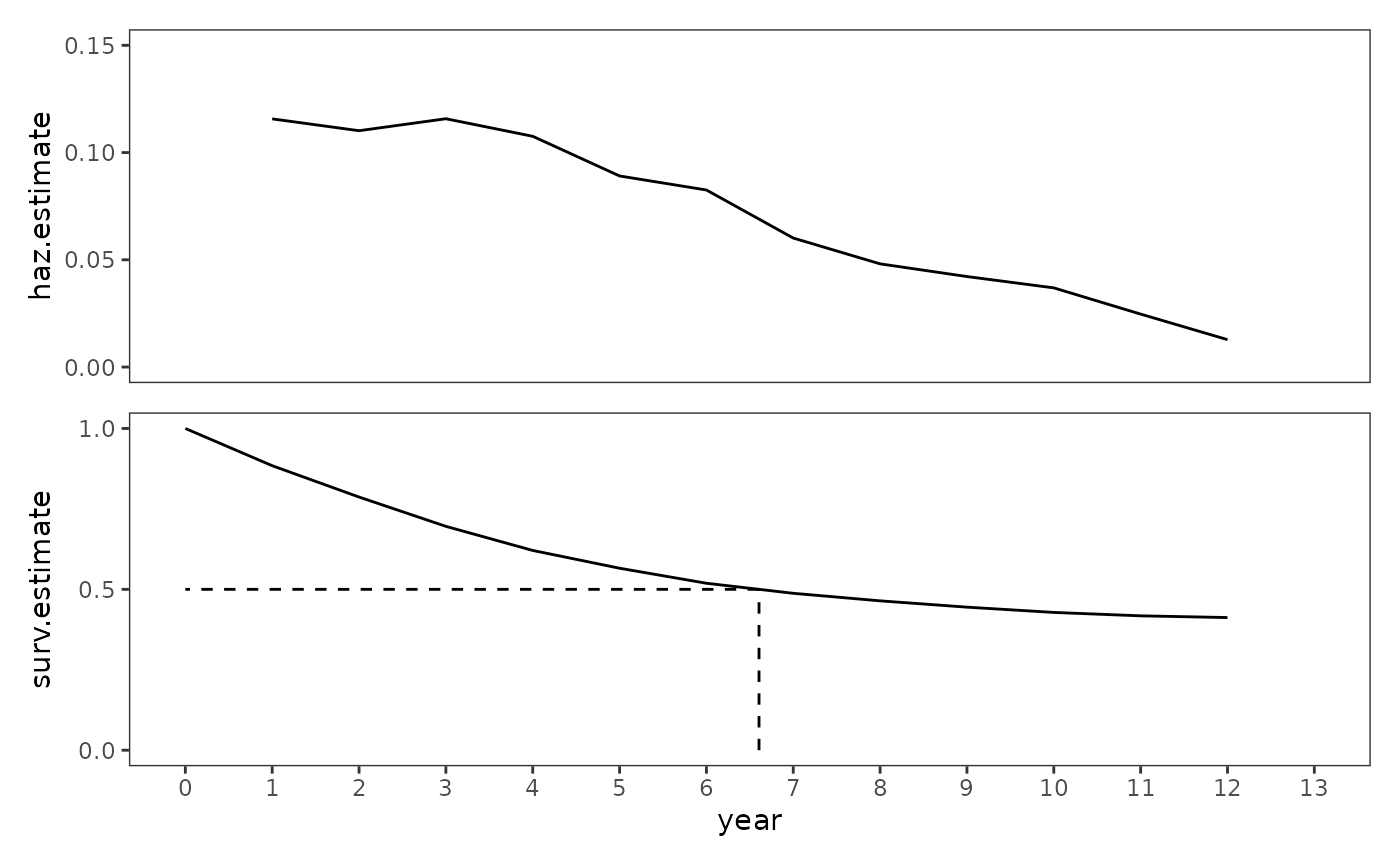

When examining plots like these, Singer and Willett (2003) recommend looking for patterns in and between the trajectories to answer questions like:

What is the overall shape of the hazard function?
When are the time periods of high and low risk?
Are time periods with elevated risk likely to affect large or small numbers of people, given the value of the survivor function?

10.3 Developing intuition about hazard functions, survivor functions, and median lifetimes

In Section 10.3 Singer and Willett (2003) examine and describe the estimated discrete-time hazard functions, survivor functions, and median lifetimes from four studies that differ by their type of target event, metric for clocking time, and underlying profile of risk:

cocaine_relapse_1: A person-level data frame with 104 rows and 4 columns containing a subset of data from Hall, Havassy, and Wasserman (1990), who measured the number of weeks of relapse to cocaine use in a sample of 104 former addicts released from an in-patient treatment program. In-patients were followed for up to 12 weeks or until they used cocaine for 7 consecutive days.

cocaine_relapse_1
#> # A tibble: 104 × 4
#>    id    weeks censor needle
#>    <fct> <dbl>  <dbl>  <dbl>
#>  1 501       2      0      1
#>  2 502      12      1      0
#>  3 503       1      0      1
#>  4 505       9      0      1
#>  5 507       3      0      1
#>  6 508       2      0      1
#>  7 509      12      1      0
#>  8 510      12      1      1
#>  9 511       1      0      1
#> 10 512       2      0      1
#> # ℹ 94 more rows

first_sex: A person-level data frame with 180 rows and 5 columns containing a subset of data from Capaldi, Crosby, and Stoolmiller (1996), who measured the grade year of first sexual intercourse in a sample of 180 at-risk heterosexual adolescent males. Adolescent males were followed from Grade 7 up to Grade 12 or until they reported having had sexual intercourse for the first time.

first_sex
#> # A tibble: 180 × 5
#>    id    grade censor parental_transition parental_antisociality
#>    <fct> <dbl>  <dbl>               <dbl>                  <dbl>
#>  1 1         9      0                   0                  1.98 
#>  2 2        12      1                   1                 -0.545
#>  3 3        12      1                   0                 -1.40 
#>  4 5        12      0                   1                  0.974
#>  5 6        11      0                   0                 -0.636
#>  6 7         9      0                   1                 -0.243
#>  7 9        12      1                   0                 -0.869
#>  8 10       11      0                   0                  0.454
#>  9 11       12      1                   1                  0.802
#> 10 12       11      0                   1                 -0.746
#> # ℹ 170 more rows

suicide_ideation: A person-level data frame with 391 rows and 4 columns containing a subset of data from Bolger and colleagues (1989) measuring age of first suicide ideation in a sample of 391 undergraduate students aged 16 to 22. Age of first suicide ideation was measured with a two-item survey asking respondents “Have you ever thought of committing suicide?” and if so, “At what age did the thought first occur to you?”

suicide_ideation
#> # A tibble: 391 × 4
#>    id      age censor age_now
#>    <fct> <dbl>  <dbl>   <dbl>
#>  1 1        16      0      18
#>  2 2        10      0      19
#>  3 3        16      0      19
#>  4 4        20      0      22
#>  5 6        15      0      22
#>  6 7        10      0      19
#>  7 8        22      1      22
#>  8 9        22      1      22
#>  9 10       15      0      20
#> 10 11       10      0      19
#> # ℹ 381 more rows

congresswomen: A person-level data frame with 168 rows and 5 columns containing data measuring how long all 168 women who were elected to the U.S. House of Representatives between 1919 and 1996 remained in office. Representatives were followed for up to eight terms or until 1998.

congresswomen
#> # A tibble: 168 × 5
#>    id    name                   terms censor democrat
#>    <fct> <chr>                  <dbl>  <dbl>    <dbl>
#>  1 1     Abzug, Bella               3      0        1
#>  2 2     Andrews, Elizabeth         1      0        1
#>  3 3     Ashbrook, Jean             1      0        0
#>  4 4     Baker, Irene               1      0        0
#>  5 5     Bentley, Helen             5      0        0
#>  6 6     Blitch, Iris               4      0        1
#>  7 7     Boggs, Corinne             8      1        1
#>  8 8     Boland, Veronica Grace     1      0        1
#>  9 9     Bolton, Frances            8      1        0
#> 10 10    Bosone, Reva               2      0        1
#> # ℹ 158 more rows

We can plot the discrete-time hazard functions, survivor functions, and median lifetimes from each of these four studies in a single call using the pmap() function from the purrr package.

study_plots <- pmap(
  list(
      list("cocaine_relapse_1", "first_sex", "suicide_ideation", "congresswomen"),
      list(cocaine_relapse_1, first_sex, suicide_ideation, congresswomen),
      list("weeks", "grade", "age", "terms"),
      list(0, 6, 5, 0)
  ),
  \(.title, .study, .time, .beginning) {
    
    # Get life table statistics.
    study_fit <- survfit(Surv(.study[[.time]], 1 - censor) ~ 1, data = .study)
    
    study_lifetable <- study_fit |>
      survfit0(start.time = .beginning) |>
      tidy() |>
      rename(surv.estimate = estimate) |>
      mutate(haz.estimate = if_else(time != .beginning, n.event / n.risk, NA))
    
    study_median_lifetime <- study_lifetable |>
      slice(max(which(surv.estimate >= .5)), min(which(surv.estimate <= .5))) |>
      mutate(m = c("before", "after")) |>
      select(m, time, surv = surv.estimate) |>
      pivot_wider(names_from = m, values_from = c(time, surv)) |>
      summarise(
        surv.estimate = .5,
        time = time_before
          + ((surv_before - .5) / (surv_before - surv_after))
          * (time_after - time_before)
      )
    
    # Plot discrete-time hazard and survival functions.
    study_haz <- ggplot(study_lifetable, aes(x = time, y = haz.estimate)) +
      geom_line() +
      xlab(.time)
    
    study_surv <- ggplot(study_lifetable, aes(x = time, y = surv.estimate)) +
      geom_line() +
      geom_segment(
        aes(xend = time, y = 0, yend = .5),
        data = study_median_lifetime,
        linetype = 2
      ) +
      geom_segment(
        aes(xend = .beginning, yend = .5),
        data = study_median_lifetime,
        linetype = 2
      ) +
      xlab(.time)
    
    wrap_elements(panel = (study_haz | study_surv)) + ggtitle(.title)
  }
)

# Figure 10.2, page 340:
wrap_plots(study_plots, ncol = 1)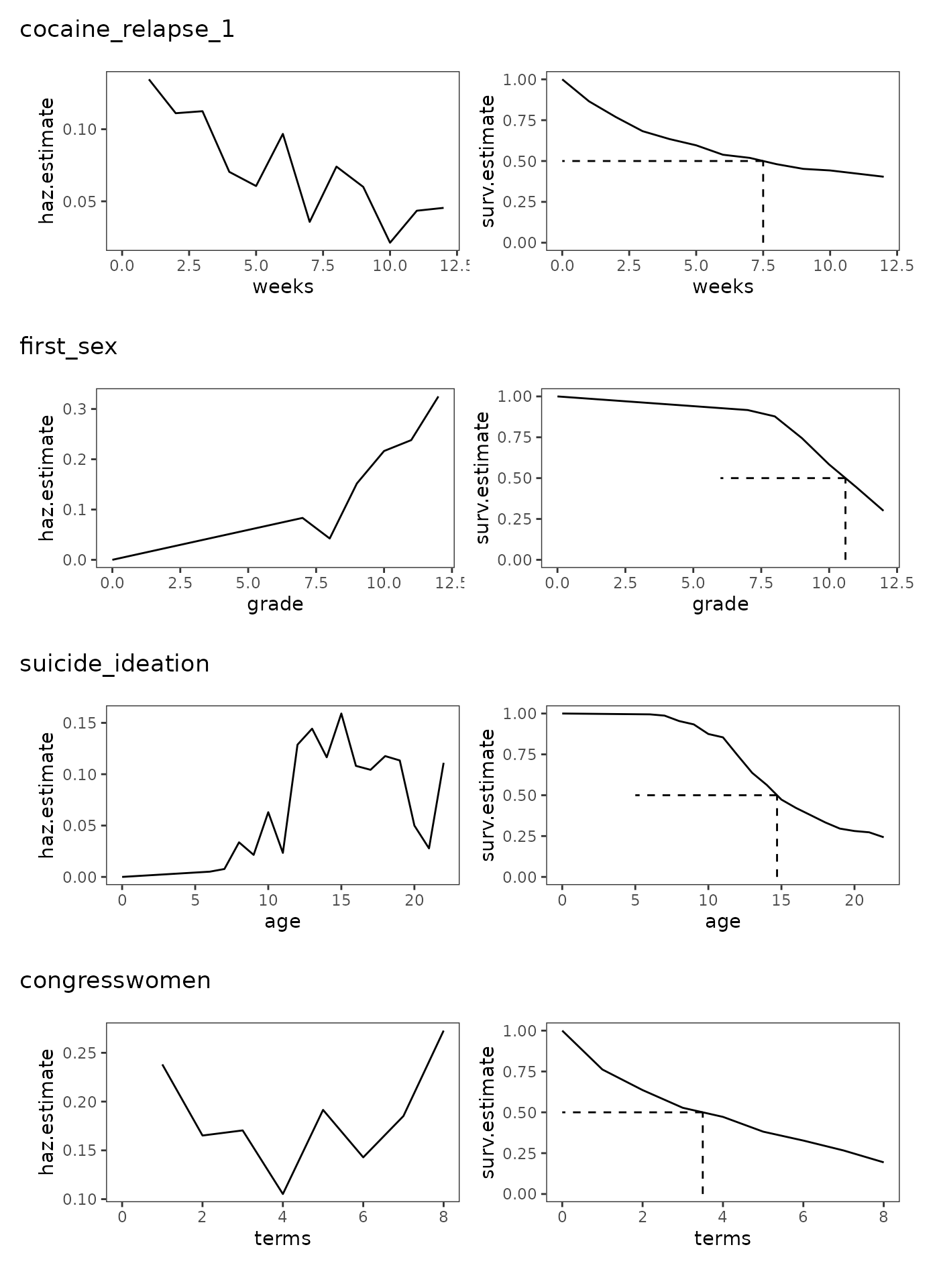

Focusing on the overall shape of the discrete-time hazard functions, and contextualizing their shape against their respective survival functions, Singer and Willet (2003) make the following observations:

cocaine_relapse_1: The discrete-time hazard function follows a monotonically decreasing pattern—peaking immediately after the “beginning of time” and decreasing thereafter—which is common when studying target events related to recurrence and relapse. This is reflected in the survival function, which drops rapidly in early time periods, then more slowly over time as the hazard decreases, indicating that the prevalence of relapse to cocaine use was greatest shortly after leaving treatment.
first_sex: The discrete-time hazard function follows a monotonically increasing pattern—starting low immediately after the “beginning of time” and increasing thereafter—which is common when studying target events that are ultimately inevitable or near universal. This is reflected in the survival function, which drops slowly in early time periods, then more rapidly over time as the hazard increases, indicating that the prevalence of first sexual intercourse in those still at risk progressively increased as time progressed.
suicide_ideation: The discrete-time hazard function follows a nonmonotonic pattern with multiple distinctive peaks and troughs, which generally arise in studies of long duration due to the data collection period being of sufficient length to capture reversals in otherwise seemingly monotonic trends. This is reflected in the survival function, which has multiple periods of slow and rapid decline, indicating that prevalence of suicide ideation was low during childhood, peaked during adolescence, and then declined near early-childhood levels in late adolescence for those still at risk.
congresswomen: The discrete-time hazard function follows a U-shaped pattern—with periods of high risk immediately after the “beginning of time” and again at the end of time—which is common when studying target events that have different causes near the beginning and end of time. This is reflected in the survival function, which drops rapidly in early and late time periods, but more slowly in the middle, indicating that prevalence of leaving office was greatest shortly after their first election, and then after having served for a long period of time for those still at risk.

10.4 Quantifying the effects of sampling variation

In Section 10.4 Singer and Willett (2003) return to the teachers data to discuss standard errors for the estimated discrete-time hazard probabilities and survival probabilities, which can also estimated directly from the life table:

Because the estimated discrete-time hazard probability is simply a sample proportion, its standard error in the $j$ th time period can be estimated using the usual formula for estimating the standard error of a proportion:

$se \big(\hat h(t_j) \big) = \sqrt{\frac{\hat h(t_j) \big(1 - \hat h(t_j) \big)}{n \text{ at risk}_j}}.$
For risk sets greater than size 20, the standard error of the survival probability in the $j$ th time period can be can be estimated using Greenwood’s approximation:

$se \big(\hat S(t_j) \big) = \hat S(t_j) \sqrt{ \frac{\hat h(t_1)}{n \text{ at risk}_1 \big(1 - \hat h(t_1) \big)} + \frac{\hat h(t_2)}{n \text{ at risk}_2 \big(1 - \hat h(t_2) \big)} + \cdots + \frac{\hat h(t_j)}{n \text{ at risk}_j \big(1 - \hat h(t_j) \big)} }.$

We estimate these standard errors here using the teachers_lifetable from Section 10.2.

# Table 10.2, page 349:
teachers_lifetable |>
  filter(year != 0) |>
  mutate(
    haz.std.error = sqrt(haz.estimate * (1 - haz.estimate) / n.risk),
    surv.std.error = surv.estimate * sqrt(
      cumsum(haz.estimate / (n.risk * (1 - haz.estimate)))
    )
  ) |>
  select(year, n.risk, starts_with("haz"), starts_with("surv"))
#> # A tibble: 12 × 6
#>     year n.risk haz.estimate haz.std.error surv.estimate surv.std.error
#>    <dbl>  <dbl>        <dbl>         <dbl>         <dbl>          <dbl>
#>  1     1   3941       0.116        0.00510         0.884        0.00510
#>  2     2   3485       0.110        0.00530         0.787        0.00652
#>  3     3   3101       0.116        0.00575         0.696        0.00733
#>  4     4   2742       0.108        0.00592         0.621        0.00773
#>  5     5   2447       0.0891       0.00576         0.566        0.00790
#>  6     6   2229       0.0825       0.00583         0.519        0.00796
#>  7     7   2045       0.0601       0.00526         0.488        0.00796
#>  8     8   1642       0.0481       0.00528         0.464        0.00800
#>  9     9   1256       0.0422       0.00567         0.445        0.00811
#> 10    10    948       0.0369       0.00612         0.428        0.00827
#> 11    11    648       0.0247       0.00610         0.418        0.00848
#> 12    12    391       0.0128       0.00568         0.412        0.00870

10.5 A simple and useful strategy for constructing the life table

In Section 10.5 Singer and Willett (2003) introduce the person-period format for event occurrence data, demonstrating how it can be used to construct the life table “by hand” using the person-level teachers data set.

The person-level data set

In the person-level format for event occurrence data, each person has only one row of data with columns for their event time and censorship status, and (optionally) a participant identifier variable or any other variables of interest. This is demonstrated in the teachers data set, A person-level data frame with 3941 rows and 3 columns:

id: Teacher ID.
years: The number of years between a teacher’s dates of hire and departure from the Michigan public schools.
censor: Censoring status.

teachers
#> # A tibble: 3,941 × 3
#>    id    years censor
#>    <fct> <dbl>  <dbl>
#>  1 1         1      0
#>  2 2         2      0
#>  3 3         1      0
#>  4 4         1      0
#>  5 5        12      1
#>  6 6         1      0
#>  7 7        12      1
#>  8 8         1      0
#>  9 9         2      0
#> 10 10        2      0
#> # ℹ 3,931 more rows

Note that unlike when modelling change, the person-level data set does not contain multiple columns for each time period; thus, as we will demonstrate below, a new strategy is needed to convert a person-level data set into a person-period data set. Additionally, and also unlike when modelling change, the person-level data set is often useful for analyzing event occurrence—as we have demonstrated through several examples in the current and previous chapter.

The person-period data set

In the person-period format for event occurrence data, each person has one row of data for each time period when they were at risk, with a participant identifier variable for each person, and an event-indicator variable for each time period.

We can use the reframe() function from the dplyr package to convert a person-level data set into a person-period data set. The reframe() function works similarly to dplyr’s summarise() function, except that it can return an arbitrary number of rows per group. We take advantage of this property to add rows for each time period when individuals were at risk, then use the information stored in these new rows and the person-level data set to identify whether an event occurred in each individual’s last period, given their censorship status.

teachers_pp <- teachers |>
  group_by(id) |>
  reframe(
    year = 1:years,
    event = if_else(year == years & censor == 0, true = 1, false = 0)
  )

teachers_pp
#> # A tibble: 24,875 × 3
#>    id     year event
#>    <fct> <int> <dbl>
#>  1 1         1     1
#>  2 2         1     0
#>  3 2         2     1
#>  4 3         1     1
#>  5 4         1     1
#>  6 5         1     0
#>  7 5         2     0
#>  8 5         3     0
#>  9 5         4     0
#> 10 5         5     0
#> # ℹ 24,865 more rows

Following similar logic, we can use the summarise() function from the dplyr package to convert a person-period data set to person-level data set.

teachers_pl <- teachers_pp |>
  group_by(id) |>
  summarise(
    years = max(year),
    censor = if_else(all(event == 0), true = 1, false = 0)
  )

teachers_pl
#> # A tibble: 3,941 × 3
#>    id    years censor
#>    <fct> <int>  <dbl>
#>  1 1         1      0
#>  2 2         2      0
#>  3 3         1      0
#>  4 4         1      0
#>  5 5        12      1
#>  6 6         1      0
#>  7 7        12      1
#>  8 8         1      0
#>  9 9         2      0
#> 10 10        2      0
#> # ℹ 3,931 more rows

The difference between the person-level and person-period formats is best seen by examining the data from a subset of individuals with different (censored) event times.

# Figure 10.4, page 353:
filter(teachers_pl, id %in% c(20, 126, 129))
#> # A tibble: 3 × 3
#>   id    years censor
#>   <fct> <int>  <dbl>
#> 1 20        3      0
#> 2 126      12      0
#> 3 129      12      1

teachers_pp |>
  filter(id %in% c(20, 126, 129)) |>
  print(n = 27)
#> # A tibble: 27 × 3
#>    id     year event
#>    <fct> <int> <dbl>
#>  1 20        1     0
#>  2 20        2     0
#>  3 20        3     1
#>  4 126       1     0
#>  5 126       2     0
#>  6 126       3     0
#>  7 126       4     0
#>  8 126       5     0
#>  9 126       6     0
#> 10 126       7     0
#> 11 126       8     0
#> 12 126       9     0
#> 13 126      10     0
#> 14 126      11     0
#> 15 126      12     1
#> 16 129       1     0
#> 17 129       2     0
#> 18 129       3     0
#> 19 129       4     0
#> 20 129       5     0
#> 21 129       6     0
#> 22 129       7     0
#> 23 129       8     0
#> 24 129       9     0
#> 25 129      10     0
#> 26 129      11     0
#> 27 129      12     0

Using the person-period data set to construct the life table

The life table can be constructed using the person-period data set through cross-tabulation of the time period and event-indicator variables. This can be accomplished using a standard df |> group_by(...) |> summarise(...) statement with the dplyr package, where we count the number of individuals who were at risk, who experienced the target event, and who were censored for each time period. After this, statistics for summarizing the event history information of the life table can be estimated using the methods demonstrated in Section 10.2.

# Table 10.3, page 355:
teachers_pp |>
  group_by(year) |>
  summarise(
    n.risk = n(),
    n.event = sum(event == 1),
    n.censor = sum(event == 0),
    haz.estimate = n.event / n.risk
  )
#> # A tibble: 12 × 5
#>     year n.risk n.event n.censor haz.estimate
#>    <int>  <int>   <int>    <int>        <dbl>
#>  1     1   3941     456     3485       0.116 
#>  2     2   3485     384     3101       0.110 
#>  3     3   3101     359     2742       0.116 
#>  4     4   2742     295     2447       0.108 
#>  5     5   2447     218     2229       0.0891
#>  6     6   2229     184     2045       0.0825
#>  7     7   2045     123     1922       0.0601
#>  8     8   1642      79     1563       0.0481
#>  9     9   1256      53     1203       0.0422
#> 10    10    948      35      913       0.0369
#> 11    11    648      16      632       0.0247
#> 12    12    391       5      386       0.0128